Sometimes, Things Are Really Simple But We Insist on Making Them Complicated
Teaching quantum mechanics to students who have not seen the subject before can be extremely challenging. Take, for example, one of its postulates (A postulate is a statement that is assumed true without proof.):
This is the time-dependent Schrödinger equation, which describes how a system evolves in time when acted upon by a force or energy. For a situation like this, I try to remind my students of the time they were in kindergarten and the teacher taught them that 1 + 1 = 2. This is no different. Being able to accept nature the way it is can be very difficult especially when our mind has been conditioned to rationalize all the time. There are building blocks which we must assume as starting material. How we connect or assemble these blocks to create something is indeed a skill, but we must not confuse skills with fundamentals.
In General Chemistry, there are likewise fundamental concepts. An example is the Law of Definite Proportions: "A chemical compound always contains exactly the same proportion of elements by mass". One can illustrate this with the following hydrocarbons: methane and octane. By mass, methane is about 75% carbon and 25% hydrogen. Octane, on the other hand, is about 84% carbon and 16% hydrogen. In order to grasp these percentages, a student needs to be able to work with atomic and molecular masses. These are among the basic principles in chemistry. Without providing students the opportunity to work with these rudimentary, and sometimes referred to as "rote learning" practices, it is inappropriate, for example, to expect to students to tackle the problem below:
It is important to identify the fundamentals. In arithmetic, addition of numbers is as rudimentary as counting. Students nowadays in American grade schools unfortunately not only have to contend with the challenge of learning to add, but also using strategies recommended by curriculum writers. Take, for example, the following strategies:
This is the time-dependent Schrödinger equation, which describes how a system evolves in time when acted upon by a force or energy. For a situation like this, I try to remind my students of the time they were in kindergarten and the teacher taught them that 1 + 1 = 2. This is no different. Being able to accept nature the way it is can be very difficult especially when our mind has been conditioned to rationalize all the time. There are building blocks which we must assume as starting material. How we connect or assemble these blocks to create something is indeed a skill, but we must not confuse skills with fundamentals.
In General Chemistry, there are likewise fundamental concepts. An example is the Law of Definite Proportions: "A chemical compound always contains exactly the same proportion of elements by mass". One can illustrate this with the following hydrocarbons: methane and octane. By mass, methane is about 75% carbon and 25% hydrogen. Octane, on the other hand, is about 84% carbon and 16% hydrogen. In order to grasp these percentages, a student needs to be able to work with atomic and molecular masses. These are among the basic principles in chemistry. Without providing students the opportunity to work with these rudimentary, and sometimes referred to as "rote learning" practices, it is inappropriate, for example, to expect to students to tackle the problem below:
Why is compressed natural gas (mostly methane, CH4) advertised as friendlier to the earth’s climate than gasoline (take octane, C8H18, for example)? The heats of combustion of methane and octane are 800 and 5000 kJ mol-1, respectively.The question does require a higher level of thinking, but it is inappropriate to ask when students do not even know how to evaluate percent compositions of compounds.
It is important to identify the fundamentals. In arithmetic, addition of numbers is as rudimentary as counting. Students nowadays in American grade schools unfortunately not only have to contend with the challenge of learning to add, but also using strategies recommended by curriculum writers. Take, for example, the following strategies:
- Make a 10: For example, to solve 5 + 7, a students is advised to add 5 to 5 to make 10, then subtract 5 from 7, that is 5 + 7 = (5 + 5) + (7 - 5) = 10 + 2 = 12.
- Make doubles: In this strategy, it is assumed that a student can do doubles easier, to solve 5 + 7, one breaks 7 first into 5 + 2, thus, 5 + 7 = 5 + 5 + 2.
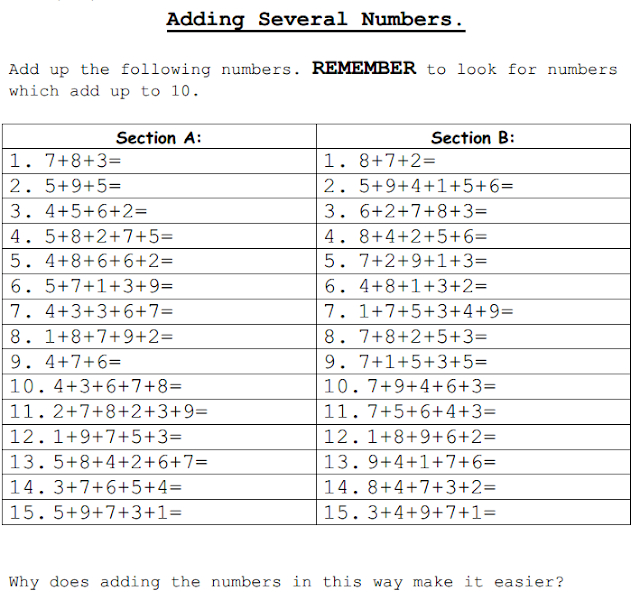
The above can be extended to adding several numbers. An example is shown below (from Thorn County Primary School):
There are children who can in fact add 7 + 8 + 3, without doing the steps recommended or in this case, "commanded", in the above exercise. And it can confuse students. Of course, in later years, being able to distribute terms in a sequence is necessary. For example, in algebra, it is useful to understand that 7x + 3 + 2x + 4 = 9x + 7. For arithmetic, we need to be more careful. Oftentimes, strategies are designed by people who already understand the process. This does not necessarily mean that it is helpful for beginners.
These strategies require that particular attention is given to each student individually. These are in fact prescriptions. Some may be appropriate, but definitely, these are not generally applicable. Ill-advised approaches also proliferate in reading. One of the fundamentals of reading is vocabulary. Yet, primary school children are likewise bombarded with strategies and interventions. First, these interventions come with their corresponding benchmark assessments. Without administering properly and correctly the assessments, these interventions may in fact harm not help a struggling student. Unfortunately, some teachers are excited to embrace seemingly fashionable strategies such as, "sound it out", "relate the story from beginning to end", without realizing that these interventions are sometimes very specific. These are interventions, no different from medicines or procedures prescribed by a physician. The wrong medicine can make things worse when prescribed and administered incorrectly or inappropriately.
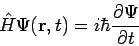
Comments
Post a Comment