Philippine Basic Education

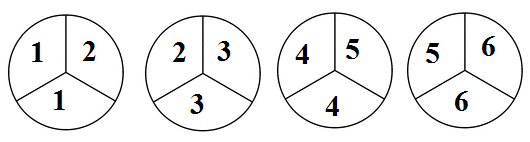
Two days ago, I had the opportunity to visit a math classroom in an elementary school. The students were working on a problem that involved division by a fraction. Each student was writing his or her solution on a worksheet and serendipitously, I observed that one student came up with an approach quite different from the others. This brought back memories from my grade school days when the teacher would ask about four students from the entire class to solve a problem on the board in front of everyone. The four are not allowed to look at each other's work and at the end, it was often enlightening to see various solutions. The specific problem the students were working on a couple of days ago was similar to this. If a bottle of vanilla extract contains 4 fluid ounces (oz.) and 2/3 oz. is required to make 1 quart of vanilla flavored ice cream, how many quarts of ice cream could I possibly make with one bottle of vanilla extract? One student was representing her solution via a drawin...

In either second or third grade of elementary school, children may be reaching the expected reading level or not.  Interventions are therefore often recommended for those who are struggling. These interventions can include lessons and strategies to help improve word recognition, fluency and spelling. These interventions may be as extensive as a one-on-one fifty minute tutoring session, five times a week. These may also take place for a period of eight months. Such intervention is, of course, expected to show good results. And it usually does. There is no argument that learning is lifelong. The question then is whether interventions need to be ongoing as well. Do interventions work in one shot? Are the effects long lasting? Blachman and coworkers have found an opportunity to answer this question by returning to an original study a decade ago. Children from several schools in New York participated in a well-controlled randomized study on how much struggling readers benefit from in...

Back in high school, we had regular weekly quizzes on current events. The quizzes were based on the contents of a bulletin that we were required to buy and read. Since the questions required a simple retrieval of information, I often read and memorized as much as I could within an hour before the quiz. After all, the quiz was only measuring a sciolistic or superficial knowledge of what was in the news. Whether I would retain the information hours after I took the quiz did not really matter. A quiz that requires only frivolous pieces of information is where cramming works best. It does not work in mathematics or in the sciences, especially when problem solving is expected. To solve problems requires first and foremost a correct choice of strategy. A final exam in chemistry, for instance, can cover so many chapters and a large part of the exam relies on a student correctly recognizing what topic is being covered by the question and choosing the appropriate approach. This is likewise tr...

" “ ... You graduated from a very good university, and you’re in a public school?” “What a waste!... ”   ... Then I realized, it’s not about my decision to be a public school teacher. It’s about what people think of our public schools. If our public schools were well run, people won’t be telling me those things." These are the words of Sabrina Ongkiko , an alumnus of Ateneo de Manila University who decided to teach in a school where a teacher's socks and shoes can be easily drenched when it rains because of leaky roofs. Sabrina correctly sums up one of the gravest ills of public basic education. Unfortunately, we are always quick to point our blaming fingers on teachers when the missteps are really from the top, education policy makers and the government. There are isolated bright spots like the story of Sabrina. Unfortunately, the image of teaching in a public school has been so tarnished that these spots can be easily overwhelmed by the darkness that currently engul...

One way a five-year old could be taught addition is by using flash cards. It is true that for some, this may sound as pure memorization. What is obviously needed is not only to remember but also to acquire the ability to relate and manipulate which then leads to a deeper understanding of arithmetic. A child of course can develop this understanding if the child has first memorized addition facts. This is not different from knowing sight words which immensely helps young minds to read. Having the facts frees up some space in a child's working memory which a child can then use to find patterns and relationships, and begin to appreciate the world of mathematics. Since a kindergarten or first grade teacher already knows what lies ahead, memorization drills can be tailored such that students can likewise anticipate what is coming. Instead of a randomly or iteratively (which may aid in memory) arranged set of flash cards, addition facts can be presented with the objective of preparing stu...

Last night, my two children and I had a mental activity. First, I recited four digits and they had to recite them in the reversed order. Both were able to do it. Then we started working on five digits. They still could do it, and we even reached seven. This is an example of measuring an individual's number storage capacity. The span of digits an individual can recall and recite backward quantifies working memory. Working memory is like a mental scratch pad on which information is both stored and manipulated. Above copied from Landmark College The following data correspond to eight-year old children. Seeing this table explains why I am a bit surprised that my son could do seven digits in reverse order. WISC-IV® DIGIT SPAN DATA FROM TABLE B.7, p. 267 Wechsler Intelligence Scale for Children -- David Wechsler © 2003 The Psychological Corporation, San Antonio TX Working memory is one characteristic that is found to correlate strongly with academic performance in the early ...

Arithmetic knowledge is as essential as literacy. Arithmetic knowledge must go beyond whole numbers since fractions or percentages appear in almost every occupation, even in fields outside of STEM (Science, Technology, Engineering and Mathematics). As a typical example, leaving a correct tip in a restaurant requires fraction arithmetic. Arithmetic knowledge involves both operation and concepts. It is important not just to know how to add, subtract, multiply and divide but also to understand what these operations really entail. After all, calculators can do all of these operations. A conceptual understanding of arithmetic operations cannot be obtained from a calculator. Such understanding is crucial to both science and engineering. It is equally advantageous for a society as a whole if individuals have a sense of what numbers and operations really mean. Arithmetic errors can be often spotted and good estimates can be made without actually performing the calculations. A more recent exa...

On one hand, we read that working together leads to better results. Take for example, a post from the blog of the United States Department of Education where a quote from a public school teacher in Springdale, Arkansas is highlighted: "I used to think about just my classroom. Now, I care about the collective whole of fourth grade." Teamwork, according to the principal in this school, has led to substantial gains in student learning simply by having teachers work as a team and believing that each student can succeed at very high levels. Watching the video above leaves me with the following phrases: "We have teachers that believe in each and every student and their potential." "We make all decisions at our school based on what the data tell us." "We are able to separate our students into who is doing really well, who is at grade level, and who is not, but not what it means by the child, but what it means by our teaching." "Ther...

My family did not have a stable source of income while I was growing up. Wearing the same pair of pants throughout the entire school week was not a matter of choice. I only had one pair of pants. I certainly would meet the description of a disadvantaged student. In addition, I was obviously an English language learner. Factors outside school were clearly not in my favor. I was aware that I was different and disadvantaged, but like any child, I desired to be like my classmates. Being wealthier, I knew, was clearly out of my reach then, but having the same aspiration and dreams, on the other hand, was within my grasp. Peer pressure is real. What happens inside one's home may seem very influential on a child but upon closer examination, chats that occur inside a playground oftentimes weigh more. A child after all spends most of his or her waking hours not at home but at school. What a child likes to watch on television is shaped by what his or her friends watch. Books that catch the...

Korea.net / Korean Culture and Information Service ( Jeon Han ) [ CC BY-SA 2.0 ], via Wikimedia Commons Full text of the message of Pope Francis to the youth University of Santo Tomas January 18, 2015 When I speak spontaneously, I do it in Spanish because I don’t know English language. May I do it? Thank you very much. Here’s Father Mark, a good translator. [As delivered by translator. Text in bold letters are spoken by the Pope himself.] The sad news today: Yesterday, as mass was about to start, a piece of the scaffolding fell. And upon falling, it hit a young woman who was working in the area, and she died. Her name is Crystal. She worked for the organization and preparation for that very mass. She was 27 years old, young like yourselves. She worked for those Catholic relief services, a volunteer worker. I would like all of you, young like her, to pray for a moment in silence with me and then we pray to Mama, our lady, in heaven. [silence] “Hail Mary, full o...

Learning mathematics can be divided into several domains. Even in the early elementary years, with regard to numeracy, three separate domains can be defined. First, pupils need to understand magnitude as expressed in numbers. Second, pupils need to acquire skills in combining numbers, as in addition and subtraction. Third, pupils need to be able to process text and construct a number sentence to calculate the unknown. These three domains: understanding, calculation, and solving word problems are very important in early elementary mathematics. At first glance, the domains may not seem entirely separate from each other. Having a "feel" for numbers, as observed even in higher education science classes, may help in both calculations as well as solving word problems. And understanding numbers by itself can manifest in different shades. For instance, the two questions shown below are quite different although both are simply assessing an understanding of numbers: Above co...

It is true that a love for reading needs to be nurtured not only in school but likewise inside children's homes. It is, however, much more practical to focus on how much a school contributes to a child's inclination to read since it is only within a school that educators could effectively draw and implement programs that enhances literacy. Schools cannot dictate what happens at home, but schools can design and support a curriculum that helps children develop a love for reading. In 2014, YouGov conducted a study for Scholastic to explore what conditions correlate with children reading books for fun. Obviously, there are various factors at home that are expected to correlate with children's reading behavior. How much a parent reads to a child is a top factor. The recent study shows that more than half (54%) of children ages 0-5 are read aloud at home 5-7 days a week. At least seventy percent of homes surveyed read a book to a child before age one. And more than eighty perc...

From the DailyMail :

Everyone Already Knows - There Is No Need to Report Anything by Joy Rizal We are now well into 2015 and at this point our children have received the following text books. English:   NOTHING FOR STUDENT USE Science:   NOTHING FOR STUDENT USE Araling Panlipunan(Social Studies):   NOTHING FOR STUDENT USE Mathematics: received paperback book week before Christmas break. Mother tongue: received paperback book week before Christmas break. Filipino: received paperback book at end of November. Mapeh:  received paperback book at the end of November. Edukasyong Pagpapakatao (character education): received paperback book at end of November. Interestingly, according to some statements made by local DepEd officials, as long as the books are received at anytime during the school year the delivery apparently counts as having been received for the students to use for the whole school year. So even though the books were only delivered at the end of the third qua...