Multiple Ways to Solve a Problem
Two days ago, I had the opportunity to visit a math classroom in an elementary school. The students were working on a problem that involved division by a fraction. Each student was writing his or her solution on a worksheet and serendipitously, I observed that one student came up with an approach quite different from the others. This brought back memories from my grade school days when the teacher would ask about four students from the entire class to solve a problem on the board in front of everyone. The four are not allowed to look at each other's work and at the end, it was often enlightening to see various solutions.
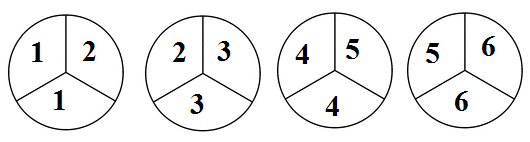
The specific problem the students were working on a couple of days ago was similar to this. If a bottle of vanilla extract contains 4 fluid ounces (oz.) and 2/3 oz. is required to make 1 quart of vanilla flavored ice cream, how many quarts of ice cream could I possibly make with one bottle of vanilla extract? One student was representing her solution via a drawing similar to this:
which meant six quarts of ice cream were possible. Four circles were drawn to represent the starting material - 4 oz. of vanilla extract. Each circle is divided into three to represent 1/3 oz and the student simply marched through the circles, writing a number on each third of the circle, starting with 1, and repeating each number once, to represent that each quart of ice cream would use 2/3 oz. The highest number reached then represented the total number of quarts of ice cream that could be made from 4 oz. of vanilla extract. The above approach was in fact the way most students took in solving the problem until I glanced at a paper of another student which showed this:
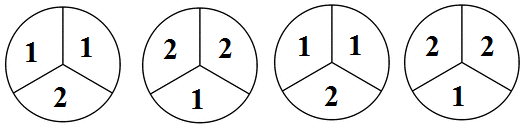
The above was obviously different from the others. In this case, the students was just writing 1's and 2's on the thirds of the circles. 1 and 2 here represented the 2/3 oz required for each quart. To find the final answer, the student must count how many 1's or 2's he or she was able to write down. Of course, this led to the same answer: 6. There were 6 instances of either 1's or 2's in the above drawing. I was impressed not only by how the student arrived at the solution, but also on how well the student was able to explain the solution to the class when asked by the teacher. The teacher then introduced on the board for the entire class to see another way of solving the problem:
The teacher then reiterated to the students why it is important to look at least at two ways of solving a math problem. The reason given is that multiple solutions provide a good way of checking if the answer is correct. If the answer obtained is the same from two different ways, chances are, the answer is correct.
Students nowadays are indeed taught to solve math problems in multiple ways. This is in line with one of the recommendations listed in the Educator's Practice Guide Improving Mathematical Problem Solving in Grades 4 through 8:
The recommendation comes only with moderate evidence because published studies on this particular approach have mixed conclusions. Although a majority points out to benefits, some are not quite significant and then there are at least three studies that point out negative effects for algebra. One reason why evidence is mixed is perhaps related to how multiple problem-solving strategies are taught.
To me, as a chemist, the more important aspect of being introduced to multiple strategies is developing flexibility. This is actually in agreement with the recommendation cited above. Developing flexibility and the skill to choose appropriate strategies should be the reason, not having a way to check if the answer is correct or not. Oftentimes, there is really one strategy that stands out from the rest. Some strategies are not transferable at all times while others are. What is then important for a student to develop is the ability to see that there may be ways that are better than the one a student has already adapted. A student may become so accustomed to one way of doing things. Later in the sciences, there are problems where only one particular strategy would work and flexibility is required in order to choose the correct strategy.
With flexibility as the objective, which clearly enhances an individual's problem-solving capacity, it becomes clear why the manner at which multiple strategies are introduced is very important. What comes with flexibility is the ability to open one's mind to various options with the ultimate goal of developing discernment. Not all strategies are made equal after all. With this goal in mind, it makes sense then that multiple ways must be introduced almost simultaneously. Focusing on one strategy can set ways in a young mind. Introducing multiple strategies in the early years allows for children to see different options before getting stuck on one. The following paper published in the British Journal of Educational Psychology provides evidence of why the manner multiple strategies are introduced matters:
In this study, students are divided into three groups. One group receives right away on the first day a lesson that compares two different strategies (Immediate-CP) . A second group is first taught extensively on one strategy and only after the students have become familiar with this strategy is a different one introduced with comparison (Delayed-CP). The third group also masters one strategy first before a different one is introduced but the two strategies are never compared against each other (Delayed-Exposure). In terms of flexibility, the results are summarized in the following graph.
The retention test in this study was administered a month later. Of course, the study not only looked at flexibility but also at how well the students actually perform in the test:
Immediate-CP does not stand out as much as in the previous figure. The authors are suggesting that with more advanced subjects (The above study worked only on an elementary algebra lesson), flexibility may factor more and may lead to better performance as problems become more complex and solutions need to be efficient, and I agree.
The specific problem the students were working on a couple of days ago was similar to this. If a bottle of vanilla extract contains 4 fluid ounces (oz.) and 2/3 oz. is required to make 1 quart of vanilla flavored ice cream, how many quarts of ice cream could I possibly make with one bottle of vanilla extract? One student was representing her solution via a drawing similar to this:
which meant six quarts of ice cream were possible. Four circles were drawn to represent the starting material - 4 oz. of vanilla extract. Each circle is divided into three to represent 1/3 oz and the student simply marched through the circles, writing a number on each third of the circle, starting with 1, and repeating each number once, to represent that each quart of ice cream would use 2/3 oz. The highest number reached then represented the total number of quarts of ice cream that could be made from 4 oz. of vanilla extract. The above approach was in fact the way most students took in solving the problem until I glanced at a paper of another student which showed this:
The above was obviously different from the others. In this case, the students was just writing 1's and 2's on the thirds of the circles. 1 and 2 here represented the 2/3 oz required for each quart. To find the final answer, the student must count how many 1's or 2's he or she was able to write down. Of course, this led to the same answer: 6. There were 6 instances of either 1's or 2's in the above drawing. I was impressed not only by how the student arrived at the solution, but also on how well the student was able to explain the solution to the class when asked by the teacher. The teacher then introduced on the board for the entire class to see another way of solving the problem:
The teacher then reiterated to the students why it is important to look at least at two ways of solving a math problem. The reason given is that multiple solutions provide a good way of checking if the answer is correct. If the answer obtained is the same from two different ways, chances are, the answer is correct.
Students nowadays are indeed taught to solve math problems in multiple ways. This is in line with one of the recommendations listed in the Educator's Practice Guide Improving Mathematical Problem Solving in Grades 4 through 8:
The recommendation comes only with moderate evidence because published studies on this particular approach have mixed conclusions. Although a majority points out to benefits, some are not quite significant and then there are at least three studies that point out negative effects for algebra. One reason why evidence is mixed is perhaps related to how multiple problem-solving strategies are taught.
To me, as a chemist, the more important aspect of being introduced to multiple strategies is developing flexibility. This is actually in agreement with the recommendation cited above. Developing flexibility and the skill to choose appropriate strategies should be the reason, not having a way to check if the answer is correct or not. Oftentimes, there is really one strategy that stands out from the rest. Some strategies are not transferable at all times while others are. What is then important for a student to develop is the ability to see that there may be ways that are better than the one a student has already adapted. A student may become so accustomed to one way of doing things. Later in the sciences, there are problems where only one particular strategy would work and flexibility is required in order to choose the correct strategy.
With flexibility as the objective, which clearly enhances an individual's problem-solving capacity, it becomes clear why the manner at which multiple strategies are introduced is very important. What comes with flexibility is the ability to open one's mind to various options with the ultimate goal of developing discernment. Not all strategies are made equal after all. With this goal in mind, it makes sense then that multiple ways must be introduced almost simultaneously. Focusing on one strategy can set ways in a young mind. Introducing multiple strategies in the early years allows for children to see different options before getting stuck on one. The following paper published in the British Journal of Educational Psychology provides evidence of why the manner multiple strategies are introduced matters:
In this study, students are divided into three groups. One group receives right away on the first day a lesson that compares two different strategies (Immediate-CP) . A second group is first taught extensively on one strategy and only after the students have become familiar with this strategy is a different one introduced with comparison (Delayed-CP). The third group also masters one strategy first before a different one is introduced but the two strategies are never compared against each other (Delayed-Exposure). In terms of flexibility, the results are summarized in the following graph.
 |
| Above copied from Bethany Rittle-Johnson et al. |
 |
| Above copied from Bethany Rittle-Johnson et al. |



Comments
Post a Comment