We Learn from Our Mistakes
Do we really learn from mistakes or does failure eventually teach us to avoid the challenge and simply give up? Using functional magnetic resonance imaging, a team of cognitive neuroscientists, Stefano Palminteri, Mehdi Khamassi, Mateus Joffily, and Giorgio Coricelli found that given the chance to reflect on our mistakes, we can turn a failure into a positive rewarding experience. Their work published in the journal Nature showed that when an individual who made a mistake was given enough information to contextualize the choices he or she had made, the brain started to switch from an avoidance circuit into the positive reward-based track for learning.
With this recent finding in mind, one can look at a study published more than a year ago by Manu Kapur, head of the Learning Sciences Lab at the National Institute of Education of Singapore, in the journal Cognitive Science with a fresh perspective. The study entitled Productive Failure in Learning Math compares two ways to teach math. Both have a problem-solving phase and an instruction phase. In one way (referred as Productive Failure (PF) in the paper), students are asked to solve problems before receiving direct instruction while in the other (referred as Direct Instruction (DI) in the paper), students receive instruction first before being asked to solve problems. The labels can be misleading but it should be made clear that in both cases, there is direct instruction. Omitting this important piece can easily lead a person to draw an erroneous conclusion from this paper.
Part of Kapur's study (the comparison between what the paper labels as PF and DI) involves seventy five students currently enrolled in ninth grade in a private school in the national capital region of India. These students are given initially a math test ability to ensure that the students when randomly assigned to either PF or DI are indeed equivalent. The scores used are from the standardized exam that the students had taken at the end of eight grade. The mean scores for each group are identical, eighty five percent. These students are getting the right answer in more than eight out of ten questions. These are evidently students that perform very well in mathematics. This sample may therefore not be representative of a general student population, another important point that should be considered when reading this paper.
The specific topic covered in the study is how to calculate standard deviation and what this value represents. After the two phases, instruction and problem solving, an assessment is administered to measure procedural knowledge, conceptual understanding, and transfer. The results for this part of the study are summarized in the following graph:
For procedural knowledge, both groups are scoring in the nineties. And as noted by Kapur, there is a probably a "ceiling effect". Students from either PF or DI are doing so well that this component of the assessment may not have been able to distinguish between the two groups. Students who either tried solving problems before being directly taught or provided instruction first before problems are obviously proficient in calculating standard deviations as shown in this assessment. This is perhaps an outcome of having only high performing students in the sample. This consideration is important as results may easily be dramatically different if the sample includes students who have been struggling in mathematics.
The other areas tested, conceptual and transfer, do indeed show an advantage of allowing students to struggle first before directly teaching them. In this case, students are clearly given the opportunity to collect what they already know in the problem solving case. Allowing for students to fail initially give them opportunities to see a lot more options including misconceptions. Thus, when direct instruction is provided later, these students are perhaps more able to see what is being taught through their own eyes and previous struggle. Students are probably not just hearing the lecture but actually listening to learn more about where they have gone wrong in their previous attempts. The students who are taught before attempting to solve problems have been guided to do things correctly and are therefore not given the chance to make their own mistakes. In a second part of the Kapur's study, a third group of students is included in which an opportunity to see other solutions including failed ones is provided. This opportunity however does not yield the same results as when the students themselves made the mistakes. It seems learning comes only from one's mistakes, and not from seeing mistakes done by others.
Learning by discovery is indeed deeper. After all, this is what doctoral studies are about. A PhD student spends most of his or her time solving a problem that has never been solved by anyone. In Kapur's experiment, it is clear that when such an approach is applied to ninth grade students who are proficient in math, Productive Failure yields better outcomes in conceptual understanding. For a PhD student, there is a mentor who guides and helps. This phase is important so that mistakes can be correctly analyzed and understood. In Kapur's experiment, this is the role direct instruction plays. Reading this paper should not lead a teacher to embrace fully Productive Failure and apply it to every classroom. The students in this study are all proficient in the procedural component. In general, this is often not the case. The lack of procedural competence is especially true in the earlier years of education when a child is just beginning to learn multiplication and division. During these years, failure can also be very devastating especially when children are not really given the chance to learn from their mistakes.
With this recent finding in mind, one can look at a study published more than a year ago by Manu Kapur, head of the Learning Sciences Lab at the National Institute of Education of Singapore, in the journal Cognitive Science with a fresh perspective. The study entitled Productive Failure in Learning Math compares two ways to teach math. Both have a problem-solving phase and an instruction phase. In one way (referred as Productive Failure (PF) in the paper), students are asked to solve problems before receiving direct instruction while in the other (referred as Direct Instruction (DI) in the paper), students receive instruction first before being asked to solve problems. The labels can be misleading but it should be made clear that in both cases, there is direct instruction. Omitting this important piece can easily lead a person to draw an erroneous conclusion from this paper.
Part of Kapur's study (the comparison between what the paper labels as PF and DI) involves seventy five students currently enrolled in ninth grade in a private school in the national capital region of India. These students are given initially a math test ability to ensure that the students when randomly assigned to either PF or DI are indeed equivalent. The scores used are from the standardized exam that the students had taken at the end of eight grade. The mean scores for each group are identical, eighty five percent. These students are getting the right answer in more than eight out of ten questions. These are evidently students that perform very well in mathematics. This sample may therefore not be representative of a general student population, another important point that should be considered when reading this paper.
The specific topic covered in the study is how to calculate standard deviation and what this value represents. After the two phases, instruction and problem solving, an assessment is administered to measure procedural knowledge, conceptual understanding, and transfer. The results for this part of the study are summarized in the following graph:
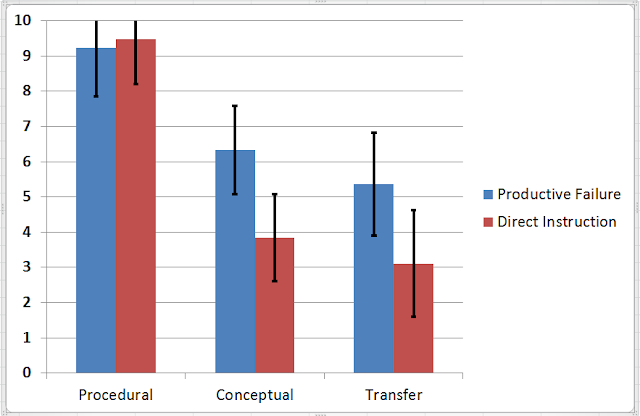 |
| Above graph drawn from data provided by Kapur, M. (2014), Productive Failure in Learning Math. Cognitive Science, 38: 1008–1022. doi: 10.1111/cogs.12107 |
For procedural knowledge, both groups are scoring in the nineties. And as noted by Kapur, there is a probably a "ceiling effect". Students from either PF or DI are doing so well that this component of the assessment may not have been able to distinguish between the two groups. Students who either tried solving problems before being directly taught or provided instruction first before problems are obviously proficient in calculating standard deviations as shown in this assessment. This is perhaps an outcome of having only high performing students in the sample. This consideration is important as results may easily be dramatically different if the sample includes students who have been struggling in mathematics.
The other areas tested, conceptual and transfer, do indeed show an advantage of allowing students to struggle first before directly teaching them. In this case, students are clearly given the opportunity to collect what they already know in the problem solving case. Allowing for students to fail initially give them opportunities to see a lot more options including misconceptions. Thus, when direct instruction is provided later, these students are perhaps more able to see what is being taught through their own eyes and previous struggle. Students are probably not just hearing the lecture but actually listening to learn more about where they have gone wrong in their previous attempts. The students who are taught before attempting to solve problems have been guided to do things correctly and are therefore not given the chance to make their own mistakes. In a second part of the Kapur's study, a third group of students is included in which an opportunity to see other solutions including failed ones is provided. This opportunity however does not yield the same results as when the students themselves made the mistakes. It seems learning comes only from one's mistakes, and not from seeing mistakes done by others.
Learning by discovery is indeed deeper. After all, this is what doctoral studies are about. A PhD student spends most of his or her time solving a problem that has never been solved by anyone. In Kapur's experiment, it is clear that when such an approach is applied to ninth grade students who are proficient in math, Productive Failure yields better outcomes in conceptual understanding. For a PhD student, there is a mentor who guides and helps. This phase is important so that mistakes can be correctly analyzed and understood. In Kapur's experiment, this is the role direct instruction plays. Reading this paper should not lead a teacher to embrace fully Productive Failure and apply it to every classroom. The students in this study are all proficient in the procedural component. In general, this is often not the case. The lack of procedural competence is especially true in the earlier years of education when a child is just beginning to learn multiplication and division. During these years, failure can also be very devastating especially when children are not really given the chance to learn from their mistakes.
Comments
Post a Comment