It's Not The Bell, It's The Bimodal That We Should Eliminate

Mike Mattos, a leader in professional learning communities, reminds educators that they must work to eliminate the "expectation that student achievement should plot across a bell-shaped curve". Of course, with the primary objective of "learning for all", a bell curve definitely points out that we are unsuccessful. The problem, however, is more serious than a bell curve. As Professor Massimo Boninsegni of Alberta pointed out years ago, a bimodal distribution is much more insidious.

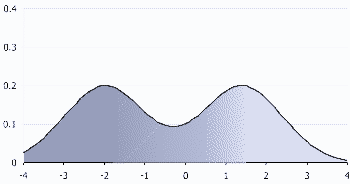A bimodal distribution

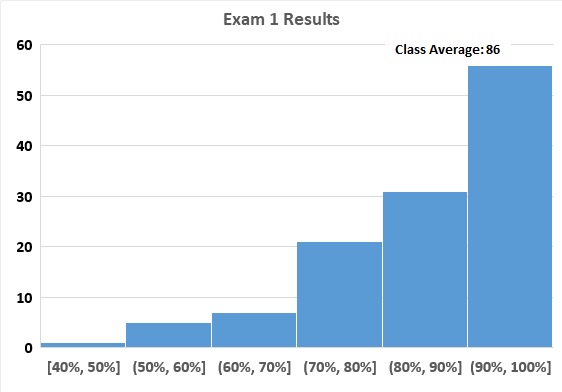
The above distribution can be seen in introductory science courses in college. A class with such a distribution can be divided into two groups. Oftentimes, the class is composed of two types of students: students who have taken advanced science courses in high school and students who have not. When such a distribution appears, it is apparent that some students are not seeing new material, while others are seeing topics for the first time. As someone who teaches an introductory chemistry course in college, I find that it is important to teach chemistry at the college level, different from high school, to avoid a bimodal distribution. I guess, I somewhat succeed. Here, for instance, is the grade distribution in a class I taught:

Fortunately, there is only one mode, and it is in the 90's.

Sadly, the bimodal distribution can become preponderant if we continue with our current mindset of advanced academics in K-12. There is obviously nothing wrong with providing opportunities for students to take advanced courses. These opportunities, however, should be tailored to a student's interest and not on some notion that a student is gifted. When we classify students according to their interests we become more intentional with our teaching. On the other hand, when we classify students according to how "smart" we think they are, the genuine purpose of teaching disappears. We are not perfect and we may not able to avoid the bell curve or normal distribution, but we must ditch the bimodal distribution especially when this bimodal distribution is correlated with family income or race.